傅里叶分析

由于晶体具有周期性的结构，因此任何具有局域特征的物理性质在平移操作$\textbf{T}=u_1\textbf{a}_1+u_2\textbf{a}_2+u_3\textbf{a}_3$下都是不变的，而对于电子数密度$n(r)$有：

$$n(r+T)=n(r)$$

考虑n在x方向上的一维周期函数$n(x)$，其周期为a，它的傅里叶展开为：

$$n(x)=n_0 +\sum_{p>0}[C_p cos(2\pi px/a)+S_p sin(2\pi px/a)]$$

其中$p$为整数，傅里叶展开系数$C_p$,$S_p$为实常量，将其写为更紧凑的形式：

$$n(x)=\sum_{p}n_p exp(i2\pi px/a)$$

将一维傅里叶分析推广到三维情况下的周期函数$n(r)$，这时，我们需要找到一组矢量$\textbf{G}$,使得

$$n(\textbf{r})=\sum_{G}n_G exp(i\textbf{G}\cdot \textbf{r})$$

在满足晶体不变性的所有晶体平移算符$\textbf{T}$作用下不变。

倒格矢

为了进一步讨论电子数密度的傅里叶分析给出的结果，必须找到$\textbf{G}$矢量。对此定义倒格矢的基矢$b_1,b_2,b_3$分别为：

$$\textbf{b}_1=2\pi \frac{\textbf{a}_2 \times \textbf{a}_3}{\textbf{a}_1 \cdot \textbf{a}_2 \times \textbf{a}_3} \\ \textbf{b}_2=2\pi \frac{\textbf{a}_3 \times \textbf{a}_1}{\textbf{a}_1 \cdot \textbf{a}_2 \times \textbf{a}_3} \\ \textbf{b}_3=2\pi \frac{\textbf{a}_1 \times \textbf{a}_2}{\textbf{a}_1 \cdot \textbf{a}_2 \times \textbf{a}_3}$$

由定义可知$\textbf{b}_1,\textbf{b}_2,\textbf{b}_3$有如下性质：

$$\textbf{b}_i \cdot \textbf{a}_j=2\pi \delta_{ij}$$

$i=j$时，$\delta_{ij}=1$，$i\ne j$时，$\delta_{ij}=0$.

在倒格子中每个倒格点可用倒格矢给出：

$$\textbf{G}=v_1 \textbf{b}_1 + v_2 \textbf{b}_2 + v_3 \textbf{b}_3$$

因此则有：

$$n(\textbf{r}+\textbf{T})=\sum_{G}n_G exp(i \textbf{G} \cdot \textbf{r}) exp(i \textbf{G} \cdot \textbf{T})$$

其中$exp(i \textbf{G} \cdot \textbf{T})=1$,因为

$$exp(i \textbf{G} \cdot \textbf{T})=exp[i(v_1 \textbf{b}_1 + v_2 \textbf{b}_2 + v_3 \textbf{b}_3) \cdot (u_1\textbf{a}_1+u_2\textbf{a}_2+u_3\textbf{a}_3)]=exp[i2\pi (v_1u_1+v_2u_2+v_3u_3)]$$

式中的指数为$2\pi i$乘上一个整数，因此

$$n(\textbf{r}+\textbf{T})=n(\textbf{r})=\sum exp(i\textbf{G} \cdot \textbf{r})$$

由此可知每个晶体结构都将有两套晶格与之相联系，分别为正晶格（正格子）与倒晶格（倒格子）。晶体结构的显微图像为实空间的真实映像，衍射图样是倒格子的映像，这点会在下面证明。

倒格子是与真实空间相联系的傅里叶空间中的晶格。

衍射条件

定理：一组倒格矢$\textbf{G}$决定了可能存在的X射线反射。

由图中可看出，对于相距为$\textbf{r}$的体积元其散射束之间的相位差因子是$exp[i(\textbf{k}-\textbf{k}^{'}) \cdot \textbf{r}]$,入射束和散射束的波矢分别为$\textbf{k}$和$\textbf{k}^{'}$。假定一个体积元散射的波振幅正比于该处的电子浓度，则在$\textbf{k}^{'}$方向上散射波的总振幅正比于$n(\textbf{r}) dV$同相位因子$exp[i(\textbf{k}-\textbf{k}^{'}) \cdot \textbf{r}]$的乘积在整个晶体体积内的积分。

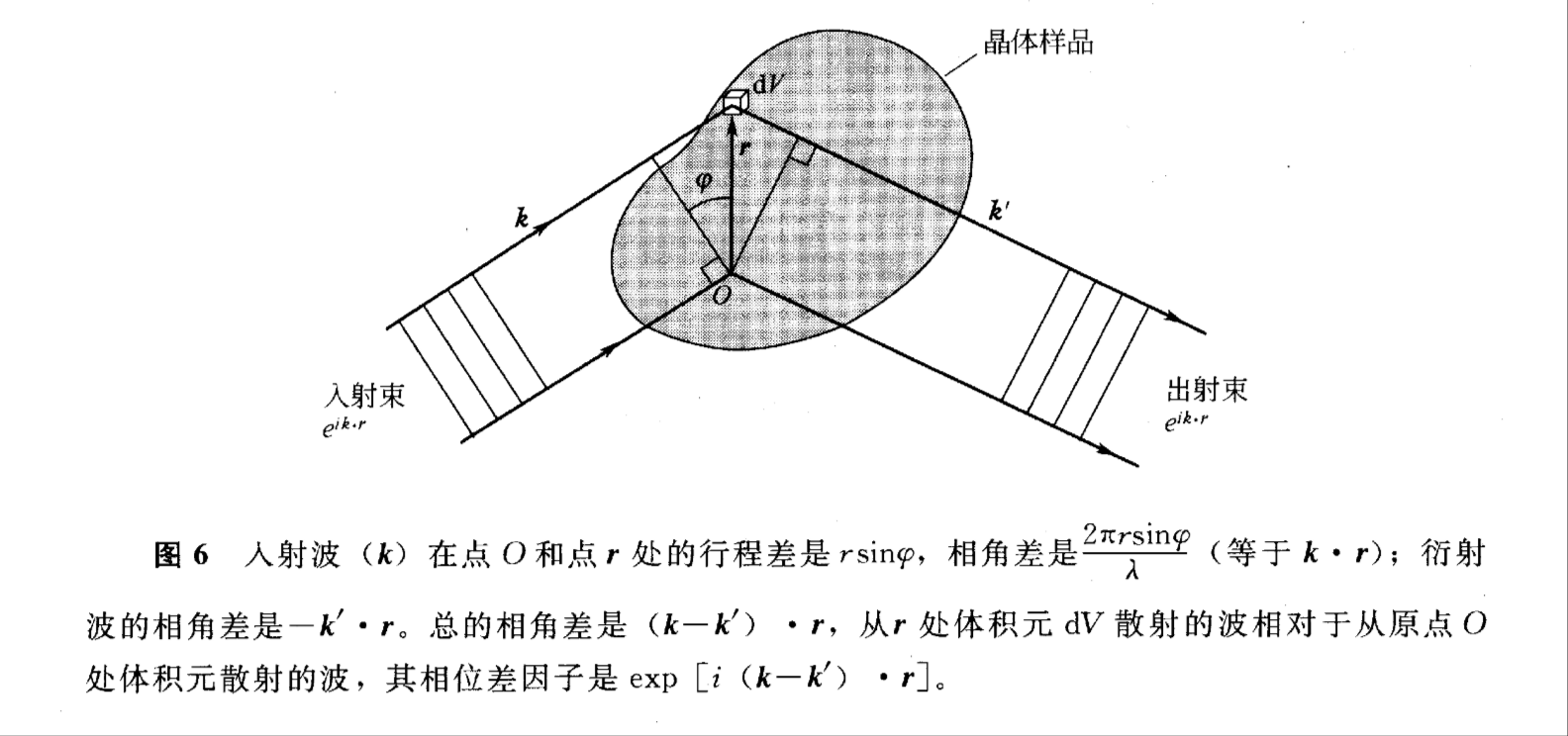
即散射电磁波的电矢量或磁矢量振幅正比于如下的积分式，其称为散射振幅

$$F=\int dVn(\textbf{r}) exp[i(\textbf{k}-\textbf{k}^{'}) \cdot \textbf{r}]=\int dVn(\textbf{r})exp(-i \Delta \textbf{k} \cdot \textbf{r})$$

式中$\textbf{k}-\textbf{k}^{'}=-\Delta \textbf{k}$,或者$\textbf{k} + \Delta \textbf{k} =\textbf{k}^{'}$

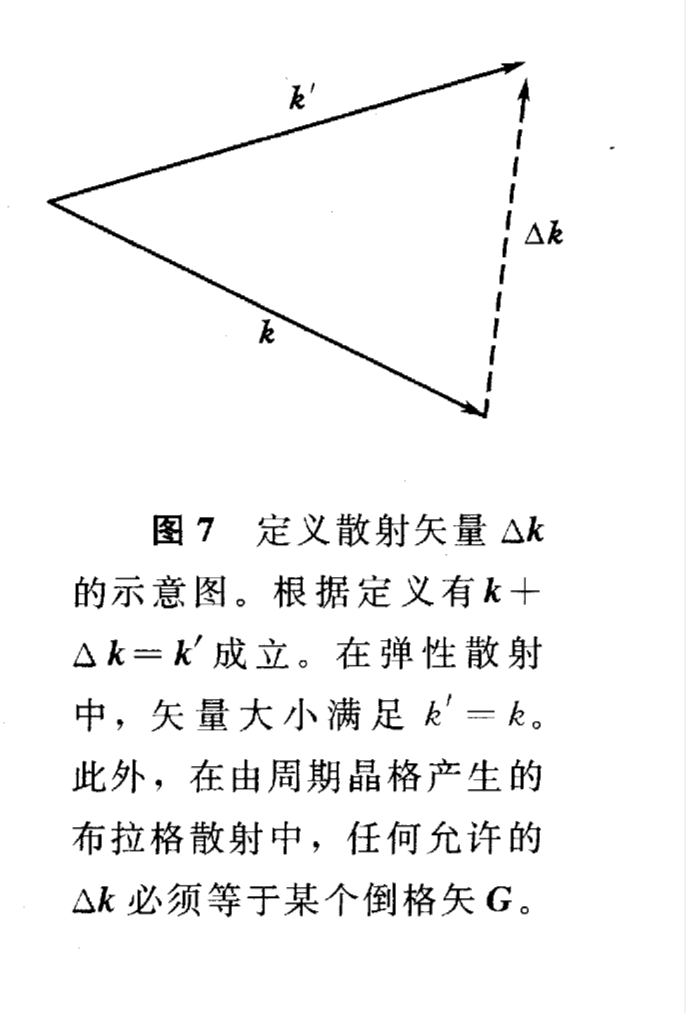
将$n(\textbf{r})$的傅里叶展开式代入积分中可得

$$F=\sum_{G}\int dV n_G exp[i(\textbf{G}-\Delta \textbf{k})\cdot \textbf{r}]$$

当散射矢量$\Delta \textbf{k}$等于一个倒格矢$\textbf{G}$时，指数的辐角变为0，而$F=V n_G$。

在弹性散射中光子能量守恒，因此出射束与入射束的频率相等，从而散射前后的波矢大小也相等，即$k=k^{'},k^2=k^{'2}$。对于电子束与中子束也同样如此，即衍射条件可写作$(\textbf{k}+\textbf{G})^2 = k^2$，或是$2\textbf{k} \cdot \textbf{G} + G^2 = 0$,又因为如果$\textbf{G}$是一个倒格矢，那么$\textbf{-G}$也为一个倒格矢，因此式子可改写为：

$$2\textbf{k} \cdot \textbf{G} = G^2$$

这一表达式常常作为产生衍射的条件，并且其为布拉格条件式的另一种表述形式。假设各位已知推论面间距$d(hkl)=\frac{2\pi}{|\textbf{G}|}$，那么上述关系式可写作

$$2(2\pi / \lambda)sin\theta = 2\pi /d(hkl)$$

或$2d(hkl)sin\theta = \lambda$。其中$\theta$为入射束与晶面之间的距离。

又因为定义$\textbf{G}$的整数hkl不一定与实际晶面指数全同，可能含有一个公因子n，由晶面指数的定义这个n已被消去，因此可得到布拉格的结果

$$2dsin\theta = n \lambda$$

劳厄方程

上述推导的结果也可用劳厄方程的形式给出，它的价值在于其于几何描述上的优势。将$\Delta \textbf{k}$和$\textbf{G}$分别与$\textbf{a}_1$,$\textbf{a}_2$,$\textbf{a}_3$进行点乘可以得到

$$\textbf{a}_1 \cdot \Delta k =2\pi v_1 \\ \textbf{a}_2 \cdot \Delta k =2\pi v_2 \\ \textbf{a}_3 \cdot \Delta k =2\pi v_3$$

这些方程的几何解释为$\Delta \textbf{k}$将在以$\textbf{a}_i$为轴的某个圆锥上，因此反射时$\Delta \textbf{k}$必须同时满足三个方向的方程,这表明三个锥必须相截交于一条公共射线。而其几何诠释图则为埃瓦尔德衍射球。

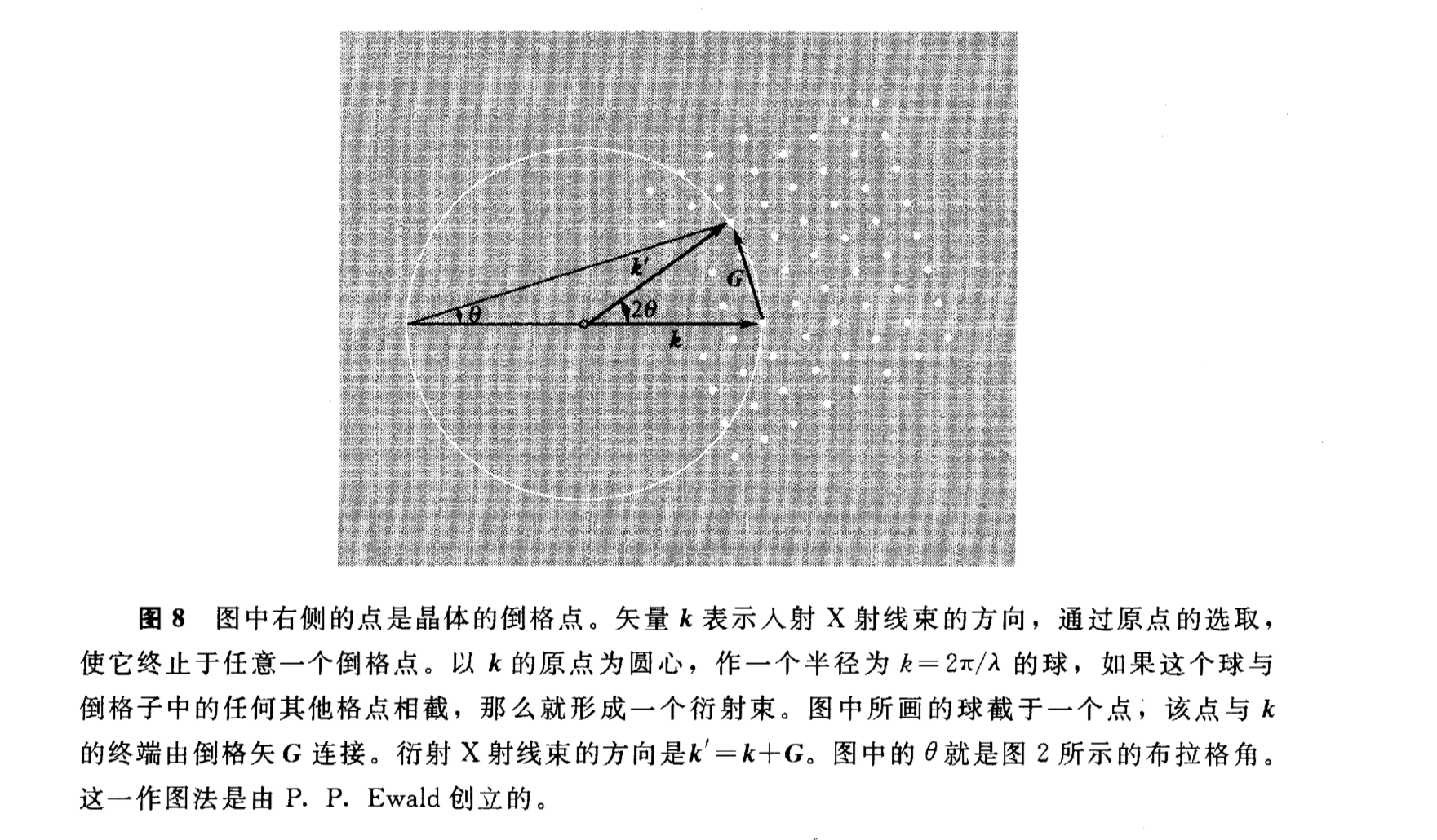
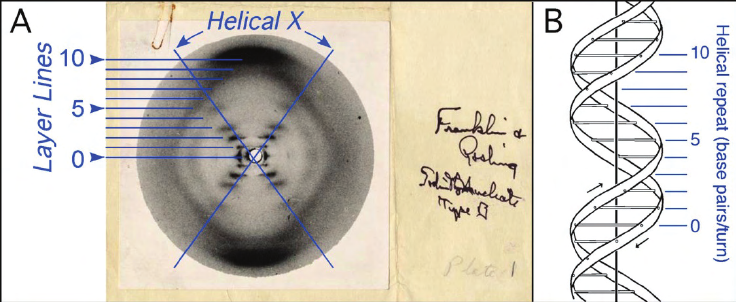
到最后还是想说一句，太伟大了劳厄，没有晶体X射线衍射的发现，就没有后续的蓬勃发展，譬如DNA的双螺旋模型的发现。

推荐书籍：《Introduction to Solid State Physics》 -----Charles Kittel